Least Squares Regression Analysis Can Help Projects
Least Squares Regression Analysis
Regression analysis is a statistical tool vastly used to investigate the relationships between variables. The study ascertains the effect of one variable on another and such analysis methods are used in various fields from engineering, economic, astronomy and even social sciences. Generally these variations are linear and this linear regression analysis of variables would indicate the likely path that may be followed by variables.
Regression or curve fitting is a method of estimating trends. A curve or line with the minimal deviation from the data points can be arrived at by the method of least squares. The best fit curve would have the least square error for deviations from the data points to the line itself.
The method of least squares is an approach for analysis when the sets of equations for determining a variable are more than the number of unknowns. In this method of least squares, the overall solution minimizes the sum of the squares obtained from the errors that are made while solving each equation. This gives the maximum likelihood of a variable assuming that the errors have a normal distribution. The method of least squares generates estimators that are used in regression analysis. A straight line or curved line is fitted into the data points so that the sum of the squares of the distance of these data points from the fitted line is minimal. Minimization can be performed either in the vertical or horizontal direction.
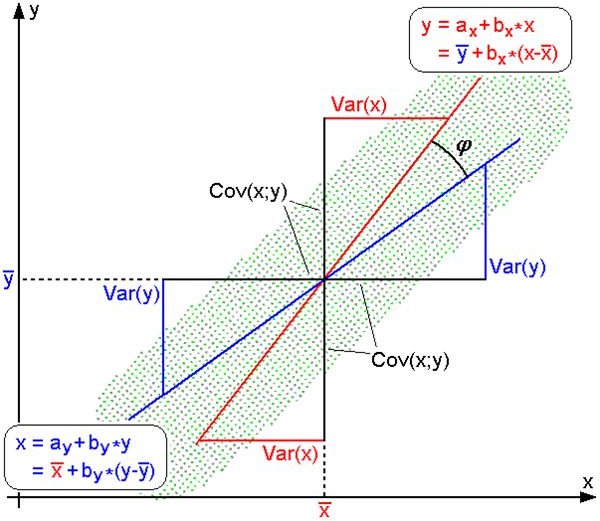
Least squares regression analysis is a method to summarize the relationship between variables. The line that goes through a path that has the least value of the sum of the squares of the deviation between the data points and the line itself is said to indicate the correct path. The line can be curved or straight depending on the sum of the least squares.
Image Source: Wikimedia
Advances That Led to Least Squares Regression Analysis
Least squares regression analysis was vastly used in the field of astronomy and was used to accurately predict the movement of celestial bodies which was necessary for ships sailing the open seas in the 18th and 19th century when land sighting was not possible.
Instead of recording a single observation with the required accuracy, it was found that taking several observations under the same conditions led to better results. These combinations were used to estimate the true value by correlating the observations with the errors. Different observations were taken under different conditions to arrive at true values based on variations and errors. Criteria were developed to determine the solution that has the least error.
Use of Least Square Regression Analysis in Project Management
Least squares regression analysis may be used to predict future trends in projects based on observations of the various parameters over time. Software is available which makes the calculation of least squares a relatively simple affair and can be used by a project manager to more accurately predict future trends whether it be in resource requirement, financial analysis, or other matters.