Understanding Stratified Random Sampling - Explanation with Example

Stratified random sampling is a probability sampling technique that requires the population to be divided into subgroups, referred to as ‘strata’, before randomly selecting the respondents from these strata. The final list of respondents must be proportional to the size of different strata, within the population. Each stratum is exclusively segmented on the basis of some variables, which are pertinent from the point of view of the research being conducted.

How Is Stratified Random Sampling Carried Out?

A simple outline of the stratified random sampling technique would entail the following steps:

1. Identifying some characteristic variable that can be used as the basis of dividing the population into subgroups.
2. Organizing the population into non-overlapping homogeneous strata.
3. The proportional size of each stratum is determined by comparing the size of the stratum with the size of the overall population.
4. Based on the total number of respondents to be covered and the proportionate size of each stratum, the final number of respondents to be picked from each stratum is identified.
5. Finally, a random selection of respondents is made from each stratum.

Where Can Stratified Random Sampling Be Used?

Stratified sampling works best in research studies where the following conditions can be satisfied:

1. The population consists of a finite number.
2. The population consists of subgroups and each of these subgroups must be investigated to increase the accuracy and reliability of the results.
3. The subgroups or strata within the population are exclusive and non-overlapping.
4. Each member of the population can be exclusively assigned to only one stratum.
5. Proportional samples can be obtained from within each stratum.

An Example of Stratified Random Sampling

Let’s take an example to get a better understanding of how stratified random sampling works. Say that the researcher wants to find out about how the cosmetic consumption pattern varies amongst air hostesses in different age brackets, employed with a particular airline.

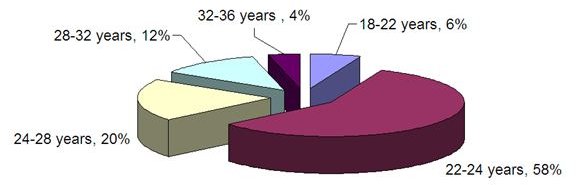
Now if the majority of the air hostesses fall in the 22-26 years age group, a random sampling will not be able to ensure that the air hostesses in other age groups are sufficiently covered. Let’s say the distribution of the air hostesses across the different age groups is something like:

• 18-22 years – 6%
• 22-24 years – 58%
• 24-28 years – 20%
• 28-32 years – 12%
• 32-36 years – 4%.

This distribution of the population has been graphically presented in the above image.

If a random sample were to be drawn from this population, it is very likely that representatives from minority groups i.e. 18-22 years and 32-36 years may be covered in very small numbers or may get completely left out. This would cause the research to go futile, as it defects the main objective of studying cosmetic use across different age groups. In keeping with the stratified random sampling approach if a sample size of 100 is to be surveyed, at least 6 air hostesses from the 18-22 age group and 4 from the 32-36 age group will be included in the survey. Once these numbers have been identified respondents can be picked up randomly from each stratum.

Thus, it’s evident from the example that using stratified random sampling, where clearly identifiable subgroups exist, lends more objectivity to the research and delivers results with higher precision for making better business decisions.

References:

1. (2009), Joan Joseph Castillo. “Stratified Sampling - Subjects Proportionally Selected From Subgroups.” The Scientific Method, Science, Research and Experiments. https://www.experiment-resources.com/stratified-sampling.html (accessed March 31, 2011).
2. " Statistics Tutorial: Stratified Random Sampling." Stat Trek: Teach yourself statistics. https://stattrek.com/Lesson6/STR.aspx (accessed March 31, 2011).

Image Credit:

Image Created by - Sidharth Thakur